Bonjour à toutes et à tous !
Il y a quelques temps, en parcourant le site Reddit, je suis tombé sur un post du subreddit r/Jokes où quelqu’un racontait la blague suivante :
Pour la plupart des gens, c’est une blague tout à fait valable. Je pense que j’aurais ri aussi, ou du moins souri, si je n’avais pas été au courant qu’il est parfaitement possible de compter jusqu’à douze, voire plus, sur une seule main – à condition d’avoir au moins quatre doigts à cette main.
Mais d’abord, comme d’habitude, un petit peu de mise en contexte.
Compter avec les doigts
Les bases
Une manière très naturelle de compter est simplement d’énumérer ce que l’on cherche à compter. Si j’ai cinq pommes devant moi, chaque pomme désignera un seul élément, un seul chiffre, et les cinq pommes formeront le nombre 5. En tout cas, en base 1 ou système unaire.
La base, en mathématiques, désigne le nombre de valeurs que peut prendre un chiffre qui compose un nombre. Notre système numérique utilise généralement la base 10, puisque nos chiffres prennent dix valeurs, allant de 0 à 9. C’est ce que l’on appelle communément le système décimal.
Qu’importe la base utilisée, lorsqu’un chiffre doit être incrémenté au-delà de sa valeur maximale, il revient à sa valeur minimale et l’on incrémente la valeur du chiffre suivant. C’est ainsi qu’en base 10 on passe, par exemple, du nombre 9 au nombre 10. (1)
En base 1, il n’y a qu’une valeur possible. Donc, pour rajouter un élément, on rajoute simplement un chiffre.
Un système pratique mais limité
C’est un système de comptage très rudimentaire, très simple. Les enfants apprennent à compter en utilisant leurs doigts. Seulement, comme vous avez dû vous en rendre compte au bout d’un moment, on se retrouve assez vite limité par le nombre de doigts : dix pour la plupart des gens, moins de dix pour les plus malchanceux et douze pour quelques rares personnes.
Les petits malins diront qu’il suffit d’utiliser ses doigts de pieds et les plus lourds diront qu’on peut ajouter encore autre chose… Mais je vais vous montrer qu’il est possible de repousser – voire carrément exploser – cette limite à deux chiffres en utilisant simplement la base 2, communément appelé le système binaire.
Compter MIEUX avec les doigts
Pour passer de la base 1 à la base 2, c’est très simple : il suffit de rajouter une valeur possible à nos chiffres. Pour un doigt, il suffit de prendre en compte l’état du doigt : baissé pour la valeur 0 et levé pour la valeur 1.
En pratique, cela donne ceci :
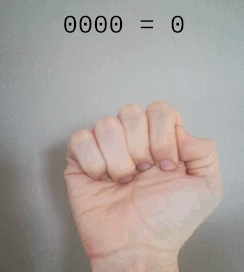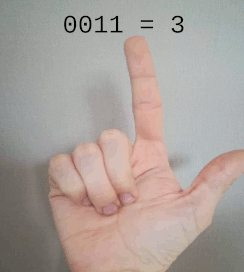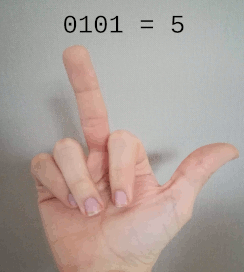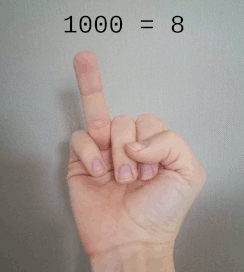
Décompte de 0 à 8, en binaire, avec les doigts d’une seule main
Notez que c’est déjà un peu plus optimal puisqu’en base 1 les doigts baissés sont tout simplement inutiles.
Si on se perd dans son comptage, il est possible de reconstituer le nombre en utilisant un peu de calcul mental. Chaque chiffre peut être multiplié par sa base portée à la puissance de sa position – si ce n’est pas clair, je vais expliquer, ne vous inquiétez pas – et, si l’on fait la somme de chaque résultat, on obtient le nombre final. Par exemple, en base 10, pour le nombre 123, nous avons :
1 × 102 + 2 × 101 + 3 × 100
=
1 × 100 + 2 × 10 + 3 × 1
=
100 + 20 + 3
=
123
Oui, ça a l’air ridicule de dire « 123 = 123 » mais je vous rappelle que c’est un système que l’on utilise couramment, au point que pour lire un nombre dans une base autre que 10, on ne peut s’empêcher de la convertir en base 10. Ainsi, pour un nombre en base 2, par exemple 101010, machinalement nous allons passer par une conversion en base 10 pour arriver à l’interpréter correctement. Et pour en revenir à la reconstitution d’un nombre binaire, ici nous avons :
1 × 25 + 1 × 23 + 1 × 21
=
1 × 32 + 1 × 8 + 1 × 2
=
32 + 8 + 2
=
42
Notez que, pour plus de clarté, j’ai ignoré les chiffres à valeur nulle, puisqu’une multiplication par 0 fait toujours 0.
Avec ce système, il est ainsi possible de compter jusqu’à 31 sur une main et 1023 sur deux mains ! Pour une main, on a multiplié notre résolution par 6 et pour deux mains par 100 ! Avouez que c’est quand même plus efficace ainsi !
Conclusion
Voilà, j’espère que cette astuce vous sera utile. Personnellement, j’utilise ce système tous les jours, c’est beaucoup plus pratique même si cela demande un peu d’entraînement pour avoir le réflexe d’utiliser ce système et pour arriver à transposer mentalement un nombre binaire en nombre décimal. C’était aussi l’occasion pour moi d’expliquer le principe du binaire de manière ludique.
N’hésitez pas à partager cette astuce si elle vous a plu.
Sur ce, je vous laisse et je vous dis à bientôt.
Nicolas SAN AGUSTIN
(1) Je fais ici une parenthèse pour rappeler une notion élémentaire : il ne faut pas confondre chiffre et nombre. Un nombre est composé d’un ou plusieurs chiffres. 1 est un chiffre et accessoirement un nombre, 10 est un nombre mais pas un chiffre – c’est un nombre à deux chiffres. Cette confusion est probablement dû à cause de l’usage abusif du terme « chiffre » dans les milieux financiers et commerciaux.
